Excel is a very handy tool to track progress and calculate averages. But data isn't always straightforward and sometimes the mean average doesn't do the job. What do you do if not all of the values are equally important?
That's where you need a weighted average.
A weighted average can give your data more meaning, and it's easy to calculate the weighted average using Excel. Here's what you need to know.
What Is a Weighted Average?
You're probably already familiar with averages. When you calculate a mean average in Excel, you add up a set of values and then divide the total by the number of values in the set. This is great when all the values equally contribute to the average. But it's not suitable when you want some values to have more impact on the resulting average.
The most likely place you will have seen weighted averages in the wild are grade calculations in school. In most courses, assignments and tests contribute differently to your overall grade. A final exam or midterm generally has a greater impact on your grade than a quiz.
Weighted averages allow you to specify how much you want something to contribute to an average. Each value is assigned a weight. The weight determines how much that value will contribute to the average. Our example will look at grades in a course.

How Do You Calculate a Weighted Average?
Weighted averages are calculated similarly to mean averages, but there are two key differences. First, you multiply the values in your number set by their weight before adding them together. Second, instead of dividing the total by the number of values in the set, you divide the total by the sum of the weights.
In our example, we would multiple the grades by their weights and add them together:
(5 * 78) + (5 * 82) + (10 * 77) + (20 * 87) + (20 * 81) + ( 40 * 75) = 7930Then, we would add up the weights:
5 + 5 + 10 + 20 + 20 + 40 = 100Now, we simply divide the total weighted values by the total weights:
7930 / 100 = 79.3So, the weighted average in this example is 79.3 percent. Knowing how to calculate the weight value by hand is useful, but time-consuming. It's far easier, and quicker, to calculate weighted averages in Excel instead.
How to Calculate a Weighted Average in Excel
Weighted averages can be calculated in the same way in Excel, as we've done below:

Column D contains the weight multiplied by the grades. Cell D2 has the command =C2*B2, D3 has =C3*B3, and so forth.
The total of the products of weight and grades is in cell D8. We calculated the total using the sum function =SUM(D2:D7), which sums all the values between D2 and D7. Similarly, the total of the weights is in cell B8, also using the SUM function.
Finally, the weighted average is calculated by dividing cell D8 by cell B8.
If this still seems like too much work, you're right! Excel offers many functions that simplify common calculations. In this case, we can use SUMPRODUCT to decrease the amount of work.
Using the SUMPRODUCT Shortcut
SUMPRODUCT does pretty much exactly what it sounds like, it returns the sum of the products of multiple data sets.
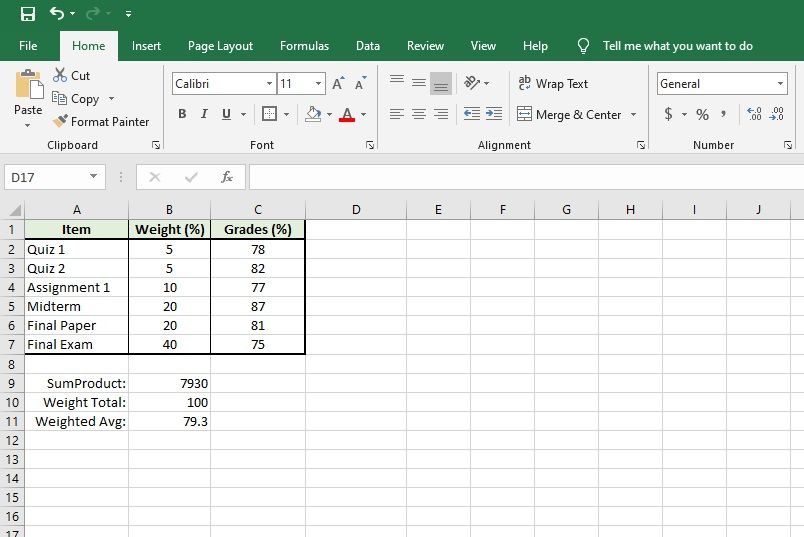
In our example, the cell B9 contains the formula: =SUMPRODUCT(B2:B7, C2:C7). SUMPRODUCT is the function call, and it requires sets of numbers to multiply and then add together.
In our example, we've given the function two data sets, the values from B2 to B7 and the values from C2 to C7. You can use as many data sets as you like, as long as each data set has the same number of values.
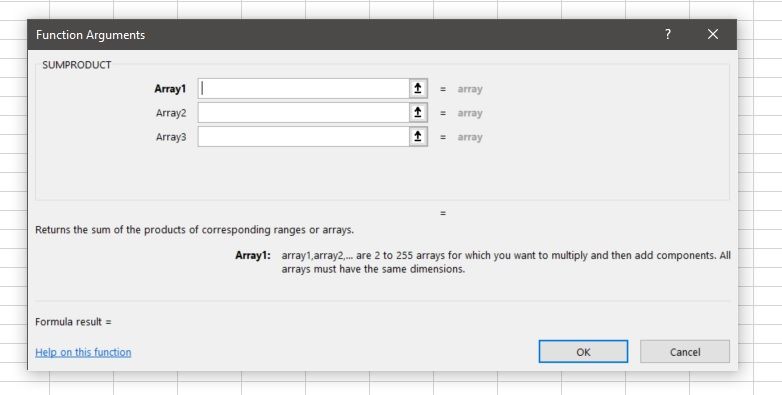
If you prefer to enter your functions using the Function Arguments window, you need to enter your data sets into the array blanks. Click on a box, then highlight the data you wish to enter. Don't worry if you have more than three data sets, as you add a data set, a new array box will appear.
SUMPRODUCT will multiply all of the first values in the data set, and add that to the product of all of the second values and so forth. Using SUMPRODUCT saves the step of multiplying each row in the columns and summing them as we did in the first example.
From here, you only need to add up the weights and divide the SUMPRODUCT by the result. To calculate the total weights, we used the SUM in the previous example.
Finally, we divided cell B9 by cell B10 to calculate the weighted average.
When to Use a Weighted Average
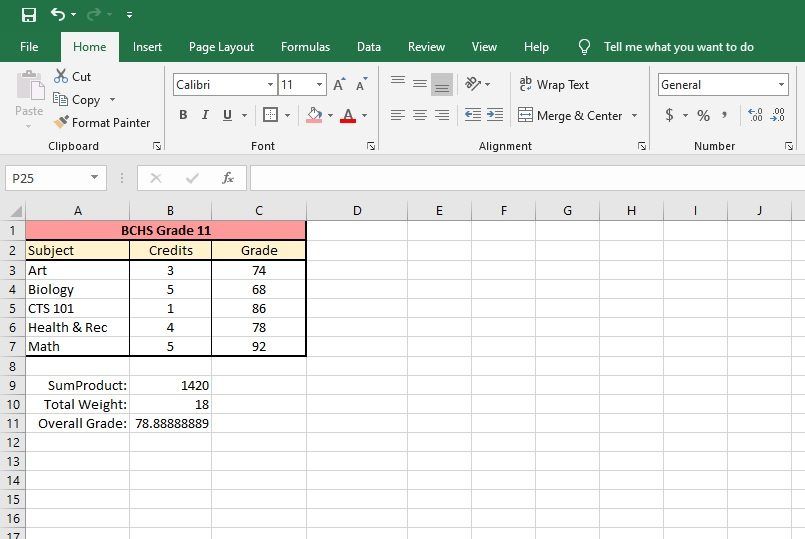
The most likely place you have seen weighted averages is in school. But aside from calculating your course average, you can also use a weighted average to calculate your grade point average across multiple courses worth different credits.
Most courses will have credit values of between 1 to 5 credits and your overall grade will be weighted by the number of credits each course is worth.
The next most common place you're likely to run into weighted averages is with sports statistics. Consider comparing the batting averages of two baseball players. The first player gets many hits, but barely any home runs. The second player gets more home runs but also has more no-hits. Which player is better?
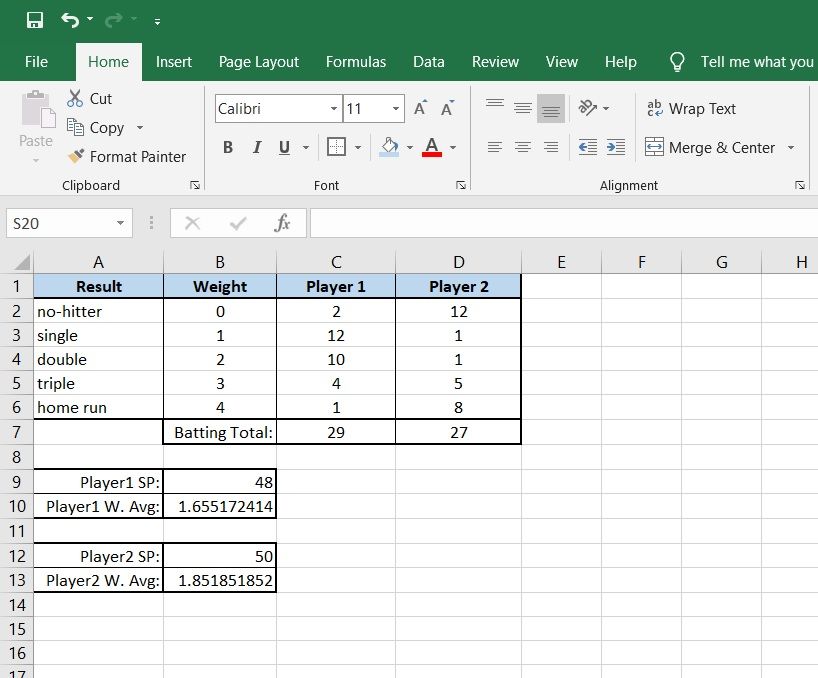
Weighted averages give a fair way to compare the two players. In our simplified batting statistics example, we found that Player 2 was the better player, despite the fact that they got many no-hits. This is because the home runs are more valuable to the team.
An important difference in this example is that we divided our SUMPRODUCT by the number of times at bat instead of the total weight. This is because we're not interested in the average over types of hits, but the average over times at bat.
Weighted averages are powerful because they allow you to compare apples to oranges. As long as you can quantify the relative values of different features, you can create a weighted average to compare different datasets.
Exploring Weighted Averages
Now that you know how to create a weighted average, you can get started analyzing your data with more accuracy. As we mentioned, calculating weighted averages in Excel is particularly valuable for teachers and students, but they have far more uses than that.
Next time you have to compare values with different levels of importance, try making a weighted average chart in Excel. It's a great way to use Excel for solving real-life problems.
Comments
Post a Comment